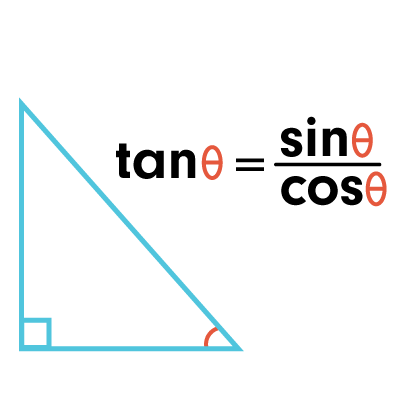In our previous grades, we have studied the methods to solve a linear equation. In this chapter, we further advance our knowledge by solving complex word problems in simpler ways. The chapter deals with finding the solution for a problem, by graphical representations as well as expressing it algebraically. Linear equations in two variables consideres …
Have you ever come across a mathematical problem which has two solutions? Woah! You must be thinking, if getting one answer was not enough, now you have to find two answers! But that’s nothing to worry, you will have so much fun learning quadratic equation. It is present in physics, for calculating the path of …
What is common between the three sequences mentioned below 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21; 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66; -27, -24, -21, -18, -15, -12, -9. All of the above sequences are Arithmetic progressions abbreviated as AP. And what do we mean by …
What is one common thing between a right-angled triangle and an isosceles triangle? Both of these figures are triangles! The concept of similarity deals with the physical appearance of any figure. If both the figures/shapes look same, although one has a comparatively larger area than the other, then the figures are called as similar structures. …
Imagine you have a sports event at your school. To conduct the running race, the rectangular school ground is divided into ten columns, each of 1m. Each column is separated by its adjacent ones with a line made up of chalk powder. On similar lines, there are 10 rows made, each of 1m, to see …
We have come across many shapes such as circle, square, triangle and the list goes on! To our surprise, the triangle holds a special place in maths. And why is that so? That’s because a complete branch of mathematics called ‘Trigonometry’ is committed to analysing triangles. In fact, the word ‘Trigonometry’ itself gives us an …
In the previous chapter, we have studied about trigonometric ratios. But ever wondered where these ratios, or say, trigonometry is used? Or what are the applications of trigonometry in our day-to-day life? Well, this is the apt location to find that out! In this chapter, we will learn numerous astonishing ways in which trigonometry is …
Try solving this riddle. I have no vertices. I have no flat faces. I have infinite axes of symmetry. Who am I? It’s a Circle. We find circular objects everywhere from round cakes and bangles, to dartboard and cycle wheels. No wonder, the world of circles takes us to another tangent. Surprisingly, tangents are exclusively …
Imagine you are constructing a bridge. The instructions given for the construction should be followed precisely. Lack of understanding may result in the bridge to collapse. So, measurements and accuracy play a key role in any construction. On similar lines, when it comes to construction in mathematics, it holds the same strategy. Firstly, we should …
Imagine a round cake. What is its area? By using the formula that we have studied in the lower grades, we can find the answer easily. But what if we tell you to to find the area of one slice of the cake? Is there a way to find its area? One slice of the …
© Copyright 2013 – 2020 Zouka Solutions Private Limited
